数据结构-堆

堆结构含义

堆是一种特殊的完全二叉树，也叫二叉堆，有两种形态，大顶堆和小顶堆

• 大顶堆，每一个节点的值都必须大于等于其子树中每个节点

• 小顶堆，每一个节点的值都必须小于等于其子树中每个节点

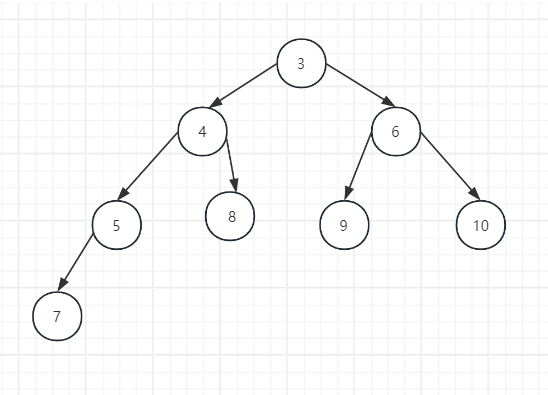
如图，是一个小顶堆，可表示为 [3, 4, 6, 5, 8, 9, 10, 7]

完全二叉树由于其结构适合用数组来存储，可以利用数组高效的随机读写，来找父子节点，比用指针更加节约空间

堆化操作

一个基于数组的二叉堆，父子节点下标之间满足一定的关系

• 父节点下标为 index，左孩子为 2*index+1，右孩子为 2*index+2

• 子节点下标为 index，父节点下标为 (index -1)/2

堆操作有两种，入堆和出堆。入堆时，会将元素追加数组后方，堆 size+1；出堆时会将数组第一个元素和最后一个有效元素交换，堆 size-1。接下来，会执行堆化操作，即节点从堆顶自上而下或从堆尾至下而上通过比较交换，找到合适位置的过程

通常将自上而下的堆化叫 heapify，自下而上的堆化叫 heapInsert

小顶堆示例代码：

public class MaxTopHeap {

    public final int[] arr;
    public int heapSize;

    public MaxTopHeap(int[] arr, int heapSize) {
        this.arr = arr;
        this.heapSize = heapSize;
    }

    /**
     * 加入新数
     * 返回最后确定的 index
     */
    public int add(int val) {
        // 加入新数
        arr[heapSize] = val;
        heapSize++;
        return heapInsert(arr, heapSize - 1);
    }

    /**
     * 删除并返回堆顶的数
     */
    public int removeTop() {
        int top = arr[0];
        swap(arr, 0, heapSize - 1);
        heapSize--;
        heapify(arr, 0, heapSize);
        return top;
    }

    /**
     * 当一个数在 index 上，尝试向上调整
     * 返回最后确定的 index
     */
    public static int heapInsert(int[] arr, int index) {
        // 计算
        int pIndex = (index - 1) / 2;
        while (arr[index] > arr[pIndex]) {
            swap(arr, index, pIndex);
            index = pIndex;
            pIndex = (pIndex - 1) / 2;
        }
        return pIndex;
    }

    /**
     * 当一个数在 index 上，尝试向下调整
     * 返回最后确定的 index
     */
    public static int heapify(int[] arr, int index, int heapSize) {
        // 左孩子
        int left = 2 * index + 1;
        while (left < heapSize) {
            int maxChildIndex = left;
            // 比较左右孩子
            if (left + 1 < heapSize) {
                maxChildIndex = arr[left + 1] > arr[left] ? left + 1 : left;
            }
            // 比较父和大孩子
            int largestIndex = arr[maxChildIndex] > arr[index] ? maxChildIndex : index;
            if (largestIndex == index) {
                break;
            }
            swap(arr, index, largestIndex);
            index = largestIndex;
            left = 2 * index + 1;
        }
        return index;
    }

    public static void swap(int[] arr, int i, int j) {
        int tmp = arr[i];
        arr[i] = arr[j];
        arr[j] = tmp;
    }
}

常见用堆的场景

堆常用来解决 TopK 问题，即在一些数据中，取出前 K 个最大（小）值

基于堆的特性，可用来排序，将要排的数据入堆再依次弹出堆顶，最终得到排好序的数组

堆排序的时间复杂度是 $O(nlogn)$​，空间复杂度是 O(1)，是不稳定排序算法

// 堆排序
public class HeapSort {

    public static void sort(int[] arr) {
        MaxTopHeap heap = new MaxTopHeap(arr, 0);
        for (int j : arr) {
            heap.add(j);
        }
        for (int i = 0; i < arr.length; i++) {
            heap.removeTop();
        }
    }
}

Java 中堆的实现是 PriorityQueue，优先队列，可以构造出大顶堆和小顶堆

PriorityQueue<Integer> minHeap = new PriorityQueue<>();
PriorityQueue<Integer> maxHeap = new PriorityQueue<>(Comparator.reverseOrder());