数据结构-图

图的概念

图是一种非线性表数据结构，类似于树，但图的节点之间可以任意连接，结构更加复杂

图的关键词：

• 顶点：图的节点一般称为顶点
• 边：顶点间互相连接的关系，根据边是否有方向，分为有向和无向
• 权：边的权重或长度
• 度：与顶点相连接的边的数量，根据边的方向，分为入度和出度

图的分类

• 按边有没有方向：有向图 / 无向图
• 按边有没有权值：带权图 / 无权图

图的表示方式

邻接矩阵

假设每个顶点都有唯一的序号，可以使用矩阵来表示图

矩阵 A 的 $A[i][j]$ 位置表示节点 i 到 节点 j 是否有边，其值代表边的权

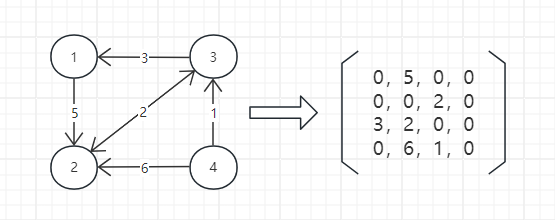
邻接矩阵可以表示有向和无向图

邻接矩阵存储方式简单，方便计算，但是当边比较稀疏时，空间浪费严重

邻接表

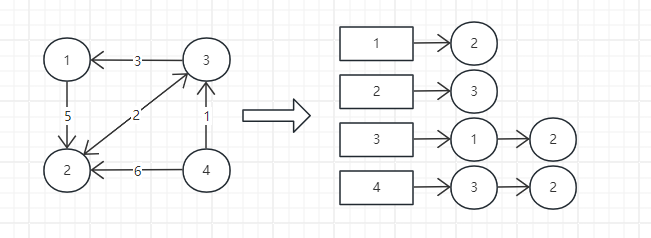
邻接表和散列表有些类似，每个顶点对应一条链表，链表中的节点是与该顶点相连接的其他顶点

邻接表也是可以表示有向和无向图

邻接表空间占用较少，但是计算时比较耗时，比如查找两顶点之间是否有连接，需要遍历链表

当然，在实际开发中可以使用其他高效的查找结构来代替链表，如有序数组、二叉查找树、散列表等

Java 表示图的经典模板

图

public class Graph {
    /**
     * 序号和点 map
     */
    public HashMap<Integer, Node> nodes = new HashMap<>();

    /**
     * 边集
     */
    public HashSet<Edge> edges = new HashSet<>();

}

顶点

public class Node {

    public int value;
    /**
     * 入度
     */
    public int in = 0;
    /**
     * 出度
     */
    public int out = 0;

    public ArrayList<Node> nexts = new ArrayList<>();
    public ArrayList<Edge> edges = new ArrayList<>();

    public Node(int value) {
        this.value = value;
    }
}

边

public class Edge {
    public int weight;

    /**
     * 起点
     */
    public Node from;

    /**
     * 终点
     */
    public Node to;

    public Edge(int weight, Node from, Node to) {
        this.weight = weight;
        this.from = from;
        this.to = to;
    }
}

示例：二维数组表示的有向图，转为上面的 Graph。此二维数组每个子数组是 $[边的权值，from 点序号，to 点序号]$

public static Graph createGraph(Integer[][] matrix) {
    Graph graph = new Graph();

    for (int i = 0; i < matrix.length; i++) {
        Integer edgeWt = matrix[i][0];
        Integer fromVal = matrix[i][1];
        Integer toVal = matrix[i][2];
        if (!graph.nodes.containsKey(fromVal)) {
            graph.nodes.put(fromVal, new Node(fromVal));

        }
        if (!graph.nodes.containsKey(toVal)) {
            graph.nodes.put(toVal, new Node(toVal));
        }
        Node from = graph.nodes.get(fromVal);
        Node to = graph.nodes.get(toVal);
        Edge edge = new Edge(edgeWt, from, to);
        graph.edges.add(edge);
        from.edges.add(edge);
        from.out++;
        to.in++;
        from.nexts.add(to);
    }

    return graph;
}

图的遍历

宽度优先遍历

宽度优先靠队列

遍历队列，遍历当前点的 nexts，每个没有被处理过的 next 都入队列

HashSet 保证不重复处理

public static void bfs(Node node) {
    Set<Node> set = new HashSet<>();
    Queue<Node> queue = new LinkedList<>();
    set.add(node);
    queue.offer(node);

    while (!queue.isEmpty()) {
        Node curr = queue.poll();
        // 模拟处理
        System.out.println(curr.value);
        // ...
        for (Node next : curr.nexts) {
            if (!set.contains(next)) {
                set.add(next);
                queue.offer(next);
            }
        }

    }
}

深度优先遍历

深度优先要用栈

每次弹出点，遍历当前点的 nexts，有一个 next 没有被处理过的，就压入当前点和该 next 并跳出 nexts 的遍历

HashSet 保证不重复处理

public static void dfs(Node node) {
    Set<Node> set = new HashSet<>();
    Stack<Node> stack = new Stack<>();
    set.add(node);
    stack.push(node);
    // 模拟处理
    System.out.println(node.value);
    while (!stack.isEmpty()) {
        Node curr = stack.pop();
        for (Node next : curr.nexts) {
            if (!set.contains(next)) {
                stack.push(curr);
                stack.push(next);
                set.add(next);
                 // 模拟处理
                System.out.println(next.value);
                // ...
                break;
            }
        }
    }
}

常见用图的场景

图适合用来表达复杂的连接关系，在实际生活中，图有着广泛的使用空间

• 编程依赖关系：Maven 的依赖、项目的顺序编译等依赖图的拓扑排序算法
• 社交关系图谱：各类社交软件的好友关系、关注等功能
• 地图：利用图的路径相关算法提供最优路径推荐
• 图数据库：超大图、大量图计算，需要靠专业的图数据库，如 Neo4j